-
Frank O. Gehry (b.1929) – Alicia Rey Alonso
Frank Gehry está considerado como uno de los más destacados representantes de la corriente desconstructivista de Estados Unidos, conocido por su particular estilo de formas semidescompuestas y su idea de que un «edificio, una vez terminado, debe ser una obra de arte, como si fuese una escultura».
Nació en Toronto, Canadá, el 28 de febrero de 1929, pero a los 15 años de edad se mudó a Estados Unidos, obteniendo más tarde la nacionalidad estadounidense. Se graduó en Arquitectura en la Universidad del Sur de California en 1954 y tras realizar el servicio militar, estudió urbanismo y planificación en la Escuela de Diseño de Harvard. A partir de entonces, Gehry comenzó a trabajar en varios estudios de arquitectura hasta el año 1961, cuando se trasladó a Paris para trabajar en el estudio de André Rémondet durante un año. Allí estudió las obras de Le Corbusier, las cuales serían una gran influencia en sus primeros trabajos.
A su vuelta a California en 1962 Gehry abrió su despacho de arquitectura, el cuál le trajo reconocimiento internacional a lo largo de los años, y es allí donde en 1969 comenzó a desarrollar su primera línea de muebles “Easy Edges”. El mobiliario está hecho de cartón prensado superpuesto en distintas direcciones para poder soportar un gran peso. “Easy Edges” se presentó en el año 1972, y ante su éxito Gehry presentó “Experimental Edges” en el año 1982.
Paralelamente, en 1972 Frank Gehry finaliza la casa estudio de Ron Davis en Malibú California, en la que se puede apreciar la mezcla de materiales y las composiciones geométricas.
En el año 1982 diseñó el Museo Aeroespacial de California el cual le dio en 1989 el Premio Pritzker, el máximo reconocimiento mundial de arquitectura, comparable al Premio Nobel. A partir de ese momento, Gehry recibe muchos encargos a lo largo de la década de los 90, tales como la Facultad de Derecho de Loyola (California), el Museo de la Universidad de Minnesota, el Centro Americano (París), Edificio Nationale Nederlanden o casa danzante (Praga), el edificio de Vitra (Basilea) y el Experience Music Project (Seattle).
Su obra más destacada de la década y probablemente de toda su carrera es el Museo Guggenheim de Bilbao el cual es uno de los mejores ejemplos de la arquitectura vanguardista del siglo pasado. Su construcción se extiende desde el año 1991 hasta el 1997, y en él se utilizaron materiales tales como cristal, acero inoxidable, zinc, o titanio, mezclados con otros no metálicos como la piedra. El diseño de este edificio conllevó que Gehry obtuviese varios premios, como el Premio Internacional de Diseño que le fue concedido por la Sociedad de Ingeniería de Iluminación de Norteamérica o la Medalla de Oro del Royal Institute of British Architects.
Durante los próximos años su obra incrementa, llegando a inaugurar más de un edificio al año. Los más destacables son el Centro de Artes Escénicas del Bard College, (Nueva York), el Walt Disney Concert Hall (Los Ángeles), el Museo Puente de Vida (Panamá), el Millenium Park, junto con el Pritzker Music Pavilion en su interior (Chicago), El centro Stata del MIT, gran ejemplo de arquitectura deconstructivista (Massachusetts), la fundación Louis Vuitton (París) y el rascacielos New York by Gehry (Nueva York).
En España, Frank Gehry diseño varios edificios, siguiendo su estilo deconstructivista, como por ejemplo el Hotel Bodega Marqués de Riscal en Álava, o la escultura de El Pez Dorado en el paseo marítimo de Barcelona.
A lo largo de su carrera, Gehry ha recibido un gran número de galardones, mencionados a continuación: Premio Dorothy and Lillian Gish, National Medal of Arts (AEB), Premio Friedrich Kiesler, Medalla de Oro del AIA, American Institute of Architects (AEB), Medalla de Oro, Royal Institute of British Architects, Gold Medal for Architecture (American Academy of Arts and Letters), Comendador de la Orden de Canadá, Medalla de Plata de Caldes de Malavella y Premio Príncipe de Asturias de las Artes.
Actualmente, a sus 87 años, Frank Gehry trabaja en su estudio Gehry Partners, LLP en Los Ángeles, California, y sigue diseñando proyectos, como el Museo Guggenheim de Abu Dabi, el cual está en construcción
Frank Gehry está considerado como uno de los arquitectos más importantes e influyentes del mundo y uno de los diez maestros de la arquitectura moderna. El arquitecto pasará a la historia por su estilo personal, que incorpora nuevas formas y materiales y es especialmente sensible con su entorno, y por haber diseñado edificios que han cambiado nuestra visión de la arquitectura vanguardista.
-
Robert Venturi (1929) & Denise Scott Brown (1931) – Gonzalo Garrido
Robert Venturi es un importante arquitecto nacido el 25 de junio de 1925 en Filadelfia (Estados Unidos). Estudió la carrera de arquitectura en la prestigiosa universidad de Princeton, la cual se sitúa en Nueva Jersey.
En cuanto a su experiencia como trabajador, al finalizar la universidad trabajó de becario durante tres años en La Academia Americana en Roma, la cual se encarga de investigar temas artísticos y es considerada una institución artística. A continuación trabajó hasta 1958 en el estudio de un arquitecto estadounidense con origen finlandés llamado Eero Saarinen y otro estadounidense llamado Louis Isadore Kahn. Mientras trabajaba para estos arquitectos fue profesor de arquitectura en otra prestigiosa universidad de Filadelfia.
Antes de casarse con Denise Scott Brown en 1967y formar un estudio en conjunto llamado «Venturi, Rauch y Scott Brown Asociados» en 1969, trabajó desde 1964 hasta 1969 con John Rauch. Además continuó siendo profesor durante treinta años en varias universidades como Harvard y Yale.
Recibió un premio muy importante comparable al premio Nobel como es el Pritzker en 1991 y en 2015/2016 la Medalla de Oro del AIA del Instituto Americano de Arquitectura junto a su mujer Denise.
Denise Scott Brown nació el 31 de octubre de 1931. Es una importante arquitecta postmoderna. Se especificó en planificación urbana y docente en universidades como Berkeley, Yale y Harvard. Está considerada como la arquitecta más famosa de la segunda mitad del siglo XX.
Estudió en primer lugar en Sudáfrica en la universidad de Witwatersrand durante 4 años la carrera de arquitectura. Allí conoció a su primer Marido llamado Robert Scott Brown, ella adoptó sus apellidos y cuando este murió de un accidente de coche y Denise se volvió a casar no cambió sus apellidos debido a que quería conservar los proyectos que había publicado con el nombre de casada.
En 1952 viajó a Londres para continuar sus estudios en la Architectural Association School of Architecture donde se graduó en 1955. Posteriormente se casó con su primer marido y estudiaron en el departamento de planificación de la Universidad de Pensilvania. En 1960 concluyó sus estudios de planificación urbana y comenzó a trabajar en la universidad donde conoció a su segundo marido Robert Venturi. Ambos empezaron a colaborar y compartieron lecciones durante dos años, después decidió dejar la universidad y fue nombrada departamento de planificación de la Universidad de Pensilvania.
En 1969 se unió a la empresa de su marido y fue nombrada directora de planificación. Actualmente es socia del estudio de arquitectura Venturi, Scott Brown y Asociados de Filadelfia que en 2012 tras la jubilación de Venturi se convirtió en VSBA Architects & Planners.
Recibió en 2015/2016 la Medalla de Oro del AIA del Instituto Americano de Arquitectura junto a su marido Robert Venturi. Y en 2013 le reconocieron el premio Pritzker el cual no se lo dieron junto a su marido en 1991 y debido a varias quejas acabaron reconociéndoselo también.
Uno de los principales objetivos de Robert y Denise al realizar sus edificios es la intención de hacerlos alegres y acabar con la monotonía dándoles un aspecto de dibujos animados usando elementos en las fachadas, colores… Se consideraban posmodernos y pretendían darle un cambio a la arquitectura haciéndola más compleja.
Tuvieron influencias de muchos sitios, incluso de ex compañeros de facultad, libros…
Algunos de sus edificios fueron casas como la Casa Vanna Venturi que fue diseñada para su madre Vanna Venturi, y construida entre los años 1962 -1964. La casa fue vendida en 1973 y sigue siendo una residencia privada. La casa de cinco habitaciones alcanza unos 9 m de altura en la parte superior de la chimenea, pero tiene una fachada monumental, efecto que se consigue mediante la manipulación intencionada de los elementos arquitectónicos que indican la escala de un edificio.
Otras obras son la Guild House la cual es una residencia de ancianos en Filadelfia, la ampliación del museo National Gallery, casas de vacaciones, Museo de Artess Manufactureras, los Juzgados de Filadelfia…
Por último, Robert publicó un manifiesto, Complejidad y contradicción en arquitectura en 1966 en el que analiza más de 200 obras arquitectónicas. Ambos publicaron más artículos y algunas obras escritas sobre temas arquitectónicos más amplios.
-
Álvaro Siza (25 de junio de 1933) – Daniel Hurtado
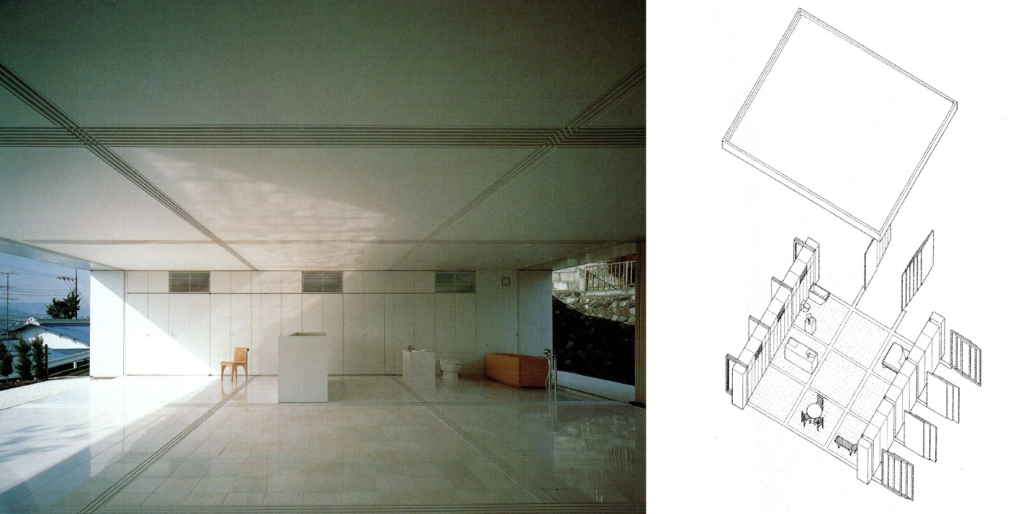
Álvaro Siza Vieira es un arquitecto portugués. Nacido en 1933 en un pueblo pesquero en Portugal, tiene un estilo muy distintivo ya presente en sus primeras obras, el Restaurante Da Boa Nova y las Piscinas en Leça de Palmeira. En ambas obras podemos ver como la obra se adapta al paisaje, usando varios niveles en vez de crear una base. También se define el estilo basado en colores claros y líneas rectas, que será evidente más adelante; el uso de la luz como parte fundamental de la obra, para añadirle volumen; y la preocupación por los habitantes de los edificios.
Se dedicó principalmente a construir viviendas sociales tras la revolución en Portugal, en las que podemos ver las características típicas de este arquitecto (uso de la luz y colores claros) muy patentes.
Dio un salto a la fama en los 80, cuando empezó a trabajar en proyectos internacionales y recibió multitud de premios. En la actualidad sigue trabajando en proyectos más variados, como museos o universidades.
-
Richard Meier (1934) – Kasija Bojanic

Richard Meier es un artista abstracto y arquitecto estadounidense. Nació en Newark, New Jersey, en 1934. Estudió arquitectura en la universidad Cornell y se graduó en 1957. A comienzos de los años 60, abrió un estudio en Nueva York donde diseñaba hospitales, viviendas, museos y edificios comerciales. Mientras, se dedicaba a dar clases en universidades de prestigio como Yale. En los siguientes años, recibe premios a nivel nacional, como el National Honor Award del Instituto Americano de Arquitectura, y se le reconoce como arquitecto de prestigio internacionalmente.
Estilo
Su propósito en sus obras es crear espacios coherentes, comprensibles y funcionales. Muestra racionalidad a través de los diseños y de su forma de pensar y analizar las alternativas que tiene.
Meier es una de los principales seguidores del movimiento racionalista del siglo XX. Una corriente que surgió a causa de la Primera Guerra Mundial en la cual se centra el interés hacia una nueva estética que rechaza la ornamentación innecesaria en la arquitectura y se caracteriza por mostrar los conceptos de estructura y función. Se usan formas geométricas simples con criterios ortogonales y la concepción dinámica de espacio. Los principios son el uso de bloques sobre pilares, las plantas bajas libres, fachada libre, colores primarios o acromáticos, ventanales alargados y terrazas-jardín. Todo esto se ve reflejado en las obras de Richard. Éstas están principalmente influidas por el arquitecto francés Le Corbusier que impuso los principios mencionados anteriormente.
Sus edificios tampoco pretenden mostrar elementos orgánicos, más bien intentan complementarse con ella manteniendo su estilo. Para él la arquitectura no es algo natural, sino algo totalmente humano y eso debe manifestarse en ella.
En las obras de Meier se manifiesta también el predominio del blanco. Esto puede parecer monótono, pero en realidad, los cambios de luz durante el día le dan diferentes matices al blanco y por ello no lo es tanto. Además, Richard defiende que las diferentes luces nos transmiten sensaciones El uso de la luz artificial para darle calidez a los interiores es un buen complemento para evitar que su arquitectura no tenga ese toque frío. Además, Richard defiende que las diferentes luces nos transmiten sensaciones y se ve reflejado en sus obras que hace un buen uso de ellas.
Obras
Iglesia del jubileo
Es su primera construcción hecha en Roma. En esta iglesia, el uso del blanco pretende dar un toque espiritual y divino transmitiendo pureza jugando con las luces que se filtran por los vidrios y claraboyas.
El proyecto se compone de dos elementos: la iglesia y el centro parroquial, en el cual hay oficinas, un auditorio y un salón de usos múltiples. Ambos edificios se hallan separados por un plano cóncavo y unidos por la mampara de cristal en la fachada del edificio.
Los elegantes arcos blancos que rodean la iglesia miden de 20 a 30 metros y están hechos de hormigón.
Museo de Artes Decorativas en Frankfurt
Después de la Segunda Guerra Mundial, muchas mansiones fueron destruidas por los bombardeos en Frackfurt. Por ello, se mandó reconstruir algunas y entre ellas figura este edificio, que posteriormente se ha convertido en museo.
En el exterior, observamos que las fachadas exteriores del edificio están hechas de placas de nevera. Los materiales utilizados son el hormigón, acero, estuco y vidrio, hace uso de ellos en muchas de sus construcciones. Gracias al estuco, se le da ese color blanco tan propio de Meier.
En este edificio se combinan el estilo de Meier y con la estructura de la mansión que había anteriormente.
Museo de Arte Contemporáneo de Barcelona (MACBA)
Richard también combina dos elementos en este edificio, combina las técnicas de la arquitectura contemporánea con las formas de los edificios contiguos al museo. El edificio también es blanco, pero las luces que internas que se ven por la noche, van cambiando de colores.
Casa Smith
Se sitúa en Darien, EEUU. Esta casa está cubierta de madera pintada de blanco, con un toque moderno y minimalista. Es luminosa y acogedora con techos altos y grandes ventanales. La casa contrasta mucho con la naturaleza que la rodea, pero tiene un toque armonioso con ella.
El Ateneo
Está en New Harmony, Indiana, EEUU, la construcción está elevada del suelo para evitar que se inunde debido a que está cerca del río Wabash. Los paneles blancos que lo rodean, son de porcelana esmaltada cuadriculada.
El centro Getty
Es el proyecto de Meier más famoso con el que se ganó una reputación. Se encuentra en Los Ángeles y ocupa 88 mil metros cuadrados. Este lote tiene elementos clásicos, no por lo estético, sino por la forma en la que se hace uso del espacio público y la organización de los edificios. Meier lo compara con una estructura aristotélica por la manera en la que se relaciona el paisaje y el lugar. Además se asemeja a la Villa de Adriano en Tivoli.
Este edificio es el único que no es blanco debido a la normativa de la ciudad. Usó un mármol travertino rústico, lo que significó un cambio radical en sus obras ya que la textura no es perfecta, sino áspera.
El propósito de este edificio es acercarse a las estructuras clásicas y de hecho, la colección del museo son esculturas griegas y romanas.
Personalmente, Richard Meier me parece un arquitecto admirable y desde luego un claro símbolo de la arquitectura racionalista. Su talento se ve reflejado en sus obras y la forma en la que las realiza muestra su inteligencia. Sin embargo, a mí personalmente me disgusta la arquitectura racionalista. Me parece casi inhumana y demasiado fría y “perfecta”. Además, me gustan los espacios más coloridos, ornamentados y con pequeños descuidos. El minimalismo y la acromía en la arquitectura dan un toque inhabitable a sus casas. Pero la gran luminosidad de ellas sí que me parece un elemento innovador que da armonía a los que las habitan.
-
Norman Foster (b. 1 June 1935) – Mar López Jarén
Norman Foster nació el 1 de Julio de 1935 en Manchester. Estudió en la Universidad de su ciudad natal, donde se sacó el grado en Arquitectura y Urbanismo en 1961. Para finalizar sus estudios, realizó un máster en la Universidad de Yale.
Aunque creció en el Reino Unido, se mudó hasta América en la primera ocasión que tuvo. Nunca estuvo de acuerdo con el conformismo de sus padres, ya que él quería conseguir los sueños y las metas que se había propuesto, mientras que sus padres estaban cómodos con sus humildes trabajos. Fue esta necesidad de tener éxito la que le impulsó a irse a América, ya que consideraba que en Estados Unidos se podía empezar de cero sin tener en cuenta el pasado. Así, en 1967, fundó con su ex mujer, Wendy Cheeseman, Foster Associates en el salón de estar de su casa, con tan solo 15 empleados.
Su carrera profesional empezó a desarrollarse en 1968, cuando trabajó por primera vez con R. Buckminster Fuller. Juntos, hicieron una serie de proyectos entre 1968 y 1983, como el Teatro Samuel Beckett, construido en 1971 en Reino Unido. En 1992, tras divorciarse de su mujer, Foster Associates se dividió, y pasó a ser Sir Norman Foster & Partners. Esto supuso un gran cambio para la empresa, ya que se construyeron sucursales en Berlín, Tokio, Hong Kong, Frankfurt y Nimes. Hoy en día, la empresa de Norman Foster ha recibido 60 premios internacionales y ha ganado 14 concursos de Arquitectura. Algunos de los mayores logros conseguidos han sido la Real Medalla de Oro de Arquitectura en 1983 y el título de Sir (caballero), otorgado por la reina, en 1990.
La mayoría de sus proyectos están construidos por el principio que él ha denominado “High Tech”, el cual se define por el uso de tecnología, de materiales ligeros y componentes industrializados. Estos elementos se repiten multitud de veces en sus proyectos. Foster pretende crear una arquitectura que elimine los componentes formales, y comience a emplear elementos más eficaces, haciendo así edificios marcados por el racionalismo y la organización, el uso de nuevos materiales y el empleo de superficies curvas.
En total, Norman Foster ha trabajado en más de 100 edificios alrededor del mundo. Sin embargo, ha trabajado también en dos proyectos no arquitectónicos: en el diseño de la mesa Nomos para Lürssen Yachts; y en la reconstrucción del coche Dymaxion, en 2010. De todo su repertorio urbanístico, los edificios más conocidos son los siguientes.
El edificio Willis, Faber & Dumas, en Inglaterra, construido entre 1970 y 1975. Es una sede de oficinas, aunque tiene una piscina y un jardín, ya que se quiso crear una mayor sensación de comodidad para los trabajadores. La estructura es ortogonal, y la fachada es una cristalera curvilínea.
El aeropuerto de Pekín, el mayor del mundo, construido entre 2003 y 2008. Se construyó para los Juegos Olímpicos de Pekín. Tiene forma de dragón, ya que se pretendía evocar a formas y colores chinos. Tiene una superficie de 1,3 millones de metros cuadrados en total.
La Torre Hearst en nueva York, construida entre el 2000 y el 2006, fue una reconstrucción de un edificio original de 6 plantas a un rascacielos de 44. Como la base del edificio está envuelta en vidrio, da la sensación de que la torre flota en el aire. Desde el exterior, tiene una estructura triangular que forma una rejilla, la cual evita en un 20% el uso del acero.
La cúpula del Reichstag, fue reconstruida en 1999. Es una estructura formada completamente por cristal, la cual tiene en su interior una escalera, la cual permite llegar hasta el tejado del edificio. Uno de los mayores problemas que hubo con este proyecto fue que, al estar formada por cristal, se creaba en su interior un efecto invernadero. Norman Foster decidió solucionar este problema añadiendo una vela en su interior, la cual gira a la misma velocidad que el sol, así consiguiendo que se bloquee parcialmente la luz del sol.
El Recinto de los Elefantes, en el Zoo de Copenhague, es otra prueba que demuestra que Norman Foster hace todo tipo de proyectos. Se quiso proporcionar a este recinto una buena ventilación, con luz suficiente pero sin crear calor excesivo y que a la vez fuera saludable para los animales y accesible y cómodo para los visitantes. Se llevó a cabo un estudio para descubrir el comportamiento de los animales. Gracias a esto, se decidió crear dos recintos separados, con zonas al aire libre y zonas cubiertas por una cúpula.
En Bilbao, diseñó las bocas de metro. Se llaman los “fosteritos”. Quería dar la sensación de que los pasajeros se estaban adentrando en una gruta, por lo que decidió hacer un diseño curvilíneo, que junto con las escaleras mecánicas, dan sensación de movimiento. Aquí, Norman Foster vuelve a emplear el vidrio, ya que es un material barato y fácil de manejar. No solo diseñó las bocas de metro, el interior de las estaciones también es diseño suyo.
La torre Swiss Re o “30 st Mary axe”, en Londres. Es una de las figuras más emblemáticas del Londres moderno. Tiene 41 plantas, y alberga en su interior desde oficinas a un centro comercial y varias salas de exposiciones en su interior. Se ensancha a medida que asciende y se vuelve a estrechar en el vértice. Foster quería crear un espacio tanto profesional como social. Por eso, en la base, tiene varios parques y zonas de ocio.
La torre Caja Madrid, de 55 plantas. De los cuatro rascacielos, es la más alta. Aquí, vuelve a utilizar en la base del edificio vidrio para dar la sensación de que está suspendido en el aire. La orientación del edificio permite aprovechar al máximo la luz solar, por lo que indirectamente, el edificio ahorra energía.
El Viaducto de Millau, en Francia. Aunque los puentes suelen ser ámbitos de ingenieros, decidió diseñarlo él. Está formado por torres que sujetan al puente mediante cables, lo que hacen que la apariencia sea fina y delicada. Supera a la torre Eiffel en cuanto a la estructura más alta de Francia (75-245 metros de altura dependiendo del tramo). Se inspiró en el ojo de una aguja para diseñar las torres.
El Ayuntamiento de Londres. Se emplearon técnicas similares que las del Reichstag para crear la forma circular. Su forma consigue que la luz solar y la ventilación de las oficinas interiores no consuman mucha energía. Para sostener la estructura, los distintos pisos tienen forma curvada en el interior, creando así un “esqueleto” para el edificio que lo sostiene.
Entrada relacionada: Arquitectos siglo XX y XXI – Jornada cultural 2016